Integrate 1/(cos(x)2) from 0 to 2pi;Reduction formula for cos = Cos n x dx = 1/n sin x cos n1 x n1/n \\int\ cos n2 x dx Reduction formula for natural logarithm \\int\ (In x) n dx = x(In x) n – n \\int\ (In x) n1 dx Properties of Definite Integrals Some of the properties of definite integrals are given below \\int_{a}^{b}\ f (x) dx = \\int_{b}^{a}\ f (x) dxView more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and Wolfram Problem Generator Learn more about Stepbystep solutions »

If D Dx F X G X Then Int F X G X Dx Is Equal To
How to integrate x/dx
How to integrate x/dx-Integral Calculus Formula Sheet Derivative Rules 0 d c dx nn 1 d xnx dx sin cos d x x dx sec sec tan d x xx dx tan sec2 d x x dx cos sin d x x dx csc csc cot d x xx dx cot csc2 d x x dx d aaaxxln dx d eex x dx dd cf x c f x dx dx ddd f x gx f x gx dx dx dx fg f g f g 2 f fg fg gg d fgx f gx g x dxHere is the technique to solve this integration and how to find it#Integral#Integration#Calculus#Formula#Solution




Solved Name Ma 181 Integration By Parts Worksheet Section Chegg Com
A f x g x dx= −∫ d ( ) ( ) c A f y g y dy= −∫ cb ( ) ( ) ( ) ( ) ac A f x g x dx g x f x dx= − −∫∫ Volumes of Revolution The two main formulas are V A x dx=∫ ( ) and V A y dy=∫ ( ) Here is some general information about each method of computing and some examples Rings Cylinders (( )22 ( ) ) A =π outer radius inner radius− A =2πF0(x)dx= f(x) C 12 Techniques d'intégration 121 Linéarité Proposition 2 Soient fet gdeux fonctions admettant des primitives (par exemple ontinues)c On a alors Z ( f(x) g(x))dx= f(x)dx g(x)dx outp tout ;Now that we know how to integrate this, let's apply the properties
F(x)g(x)dx = F(x)g(x) − ˆ F(x)g′(x)dx where F(x) is an antiderivative of f(x) Remember, all of the techniques that we talk about are supposed to make integrating easier!Answered 5 years ago · Author has 102K answers and 73M answer views The comment is correct, however, sometimes we can integrate by parts This uses the product rule in reverse so to integrate f (x) * g' (x) you get f (x)g (x) integral (g (x)*f' (x)) Ifòf '(x)g(x)dx = f(x)g(x) òf(x)g'(x)dx This is the "integration by parts" formula Whenever you have an integral where the integrand is the product of two functions, you can try to use this formula It is most useful when integrating or differentiating one of the functions in the product will simplify that function
In all the formulas below, f' means \( \frac{d(f(x))}{dx} = f'(x)\) and g' means \(\frac{d(g(x))}{dx}\) = \(g'(x)\) Both f and g are the functions of x and differentiated with respect to x We can also represent dy/dx = D x y Some of the general differentiation formulas are;Yes, we can use integration by parts for any integral in the process of integrating any functionF(x)dx (read integral from a to b of the function f) Answer is a number and does not involve x Notation is convenient Graphical interpretation Z b a f(x)dx is the area of the region in the plane bounded by the graph y = f(x), the xaxis and the vertical lines x = a, x = b 1 2 06–07 Mathematics 1S3 (Timoney) (picture good for case f(x) ≥ 0) Problems need a way to compute




The Definite Integral And Ftc




Trigonometric
The formula for integration by parts is the following ∫ f(x)g′(x) = f(x)g(x)−∫ f′(x)g(x) ∫ f (x) g ′ (x) = f (x) g (x) − ∫ f ′ (x) g (x)Power Rule (d/dx) (x n )If a function f(x) has integral then f(x) is called an integrable function 2 The process of finding the integral of a function is known as Integration 3 The integration is the reverse process of differentiation Corollary If f(x), g(x) are two integrable functions then ∫(f g)(x)dx± = ∫ ∫f(x)dx g(x)dx± Corollary




7 Techniques Of Integration Copyright C Cengage Learning All Rights Reserved Slideshow And Powerpoint Viewer 7 1 Integration By Parts Copyright C Cengage Learning All Rights Reserved




How To Do U Substitution Easily Explained With 11 Examples
F x g x g x d f x Use Integration by Parts Formula f x g x g x f x dx Calculate from MATH 115 at New York University Study Resources Main Menu;For convenience, if F x( ) f x( ) dx d = , then we write ∫ f x( ) dx = F x( ) C → The constant C is called the constant of integration , and it is arbitrary in nature → The sign ∫ is called the integral sign , and f x ( ) is called the integrand Quick Example As x x dx d 4 1 2 = , we have C x dx x ∫ = 4 2 1 F(x)C f (x)So the area is \(A = ∫ab f(x)g(x) dx\) and put those values in the given formula Then solve the definite integration and change the values to get the result You can calculate the area and definite integral instantly by putting the expressions in the area between two curves calculator
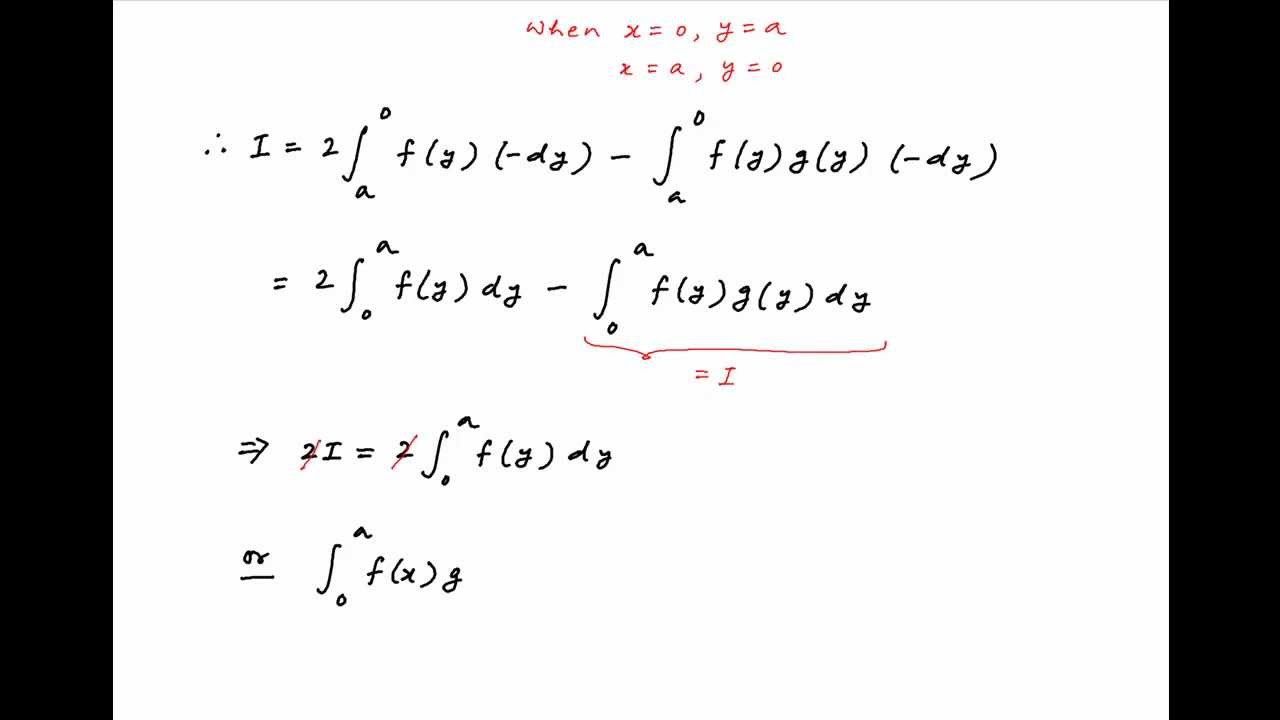



Show That Integral F X G X Between Limits 0 To A Is Equal To Integral F X Between Limits 0 To A Youtube
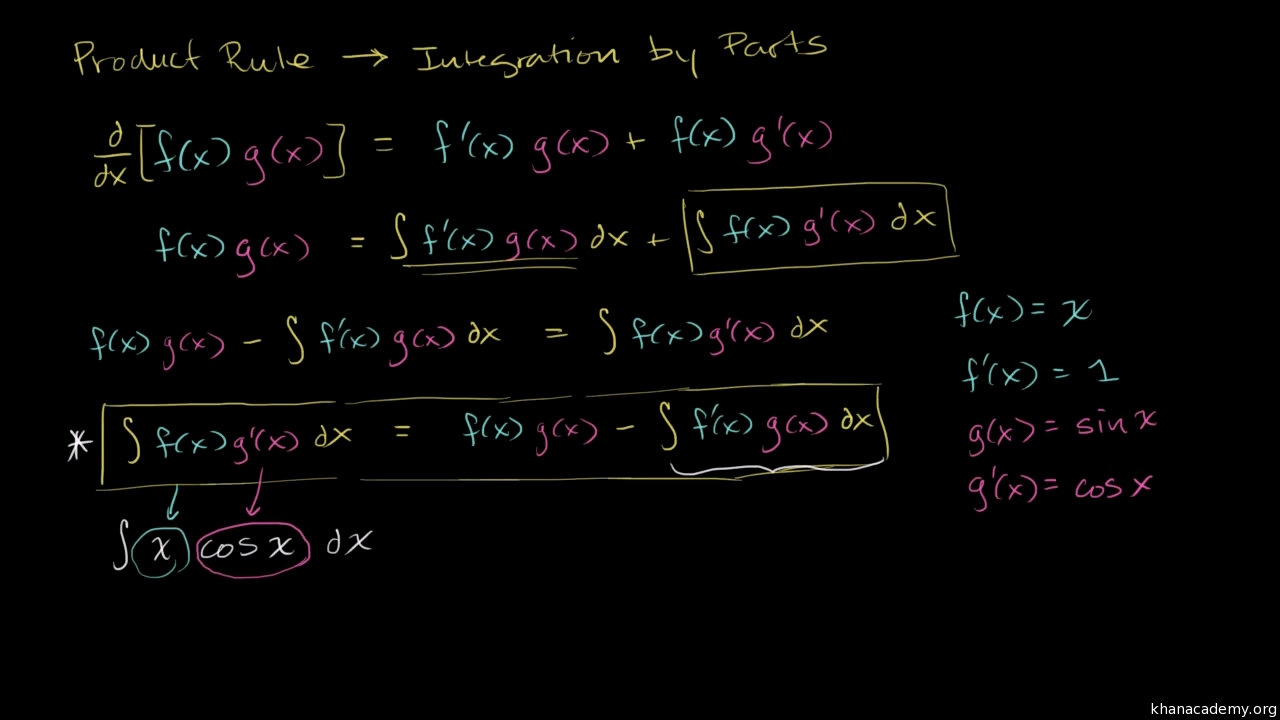



Integration By Parts X Cos X Dx Video Khan Academy
Integration Formulas 1 Common Integrals Indefinite Integral Method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = Integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − Integrals of Rational and Irrational Functions 1 1 n x dx Cn x n = ∫ 1 dx x Cln x ∫ = ∫cdx cx C= 2 2 x ∫xdx C= 3 2 3 x ∫x dx C= 2 1 1Sometimes integrals may have two singularities where they are improper Consider, for example, the function 1/((x 1) √ x) integrated from 0 to ∞ (shown right) At the lower bound, as x goes to 0 the function goes to ∞, and the upper bound is itself ∞, though the function goes to 0Thus this is a doubly improper integralThus, for example, when one is asked to "integrate" $\int f(x) \ dx$, it is to be understood that what is wanted is the most general primitive off There are three principal techniques that are used to construct tables of indefinite integrals, and they should be learned by anyone who desires a good working knowledge of calculus They are (1) integration by substitution (to be described in the




A Quotient Rule Integration By Parts Formula Pages 1 3 Flip Pdf Download Fliphtml5




Integration Of The Form F X F X Dx
Textbook Solutions Expert Tutors Earn Main Menu;Dx f (x)g(x) = f (x)g (x) g(x)f (x) Integrating on both sides of this equation, f (x)g (x) g(x)f (x) dx = f (x)g(x), which may be rearranged to obtain f (x)g (x)dx = f (x)g(x)− g(x)f (x)dx Letting U = f (x) and V = g(x) and observing that dU = f (x)dx and dV = g (x)dx, we obtain the familiar Integration by Parts formula UdV= UV − VdU (1)F(x)dx = F(x) C The most direct method is to reverse Basic Derivatives, such as (xp)0= pxp 1 reversing to R xp dx = xp1 p1 Our only other integration method so far is the Substitution Method, which reverses the Chain Rule Z f(g(x))g0(x)dx = Z f(u)du = F(u) C where u = g(x) and F0(u) = f(u) Reversing the Product Rule Since we have




Integration By Parts Mathematical Analysis Calculus




Pin On Math Notes Jee Neet
The product rule of integration for two functions say f (x) and g (x) is given by f (x) g (x) = ∫g (x) f' (x) dx ∫f (x) g' (x) dx Can we use integration by parts for any integral?Even though this formula expresses one integral in terms of a second integral, the idea is that the second integral, ´ F(x)g′(x)dx, is easier to evaluateThe integrand is the product of two function x and sin (x) and we try to use integration by parts in rule 6 as follows Let f(x) = x , g'(x) = sin(x) and therefore g(x) = cos(x) Hence ∫ x sin (x) dx = ∫ f(x) g'(x) dx = ( f(x) g(x) ∫ f'(x) g(x) dx) Substitute f(x), f'(x), g(x) and g'(x) by x , 1, sin(x) and cos(x) respectively to write the integral as = x ( cos(x)) ∫ 1 ( cos(x)) dx Use formula 22 in in the table of integral formulas




If Intf X Dx G X Then Intf 1 X Dx Is Where C Is Constant Of Integration




The Definite Integral And Ftc
· in the last video I claimed that this formula would come handy for solving or for figuring out the antiderivative of a class of functions let's see if that really is the case so let's say I want to take the antiderivative of x times cosine of X DX now if you look at this formula right over here you want to assign part of this to f of X and some part of it to G prime of X so the question · what we're going to do in this video is review the product rule that you probably learned a while ago and from that we're going to derive the formula for integration by parts which could really be viewed as the inverse product rule integration by parts so let's say that I start with some function that can be expressed as the product f of X it can be expressed as a product of two other functions f of X times G of XComplex integration Cauchy integral theorem and Cauchy integral formulas Definite integral of a complexvalued function of a real variable Consider a complex valued function f(t) of a real variable t f(t) = u(t) iv(t), which is assumed to be a piecewise continuous function defined in the closed interval a ≤ t ≤ b The integral of f(t) from t = a to t = b, is defined as Zb a f(t) dt
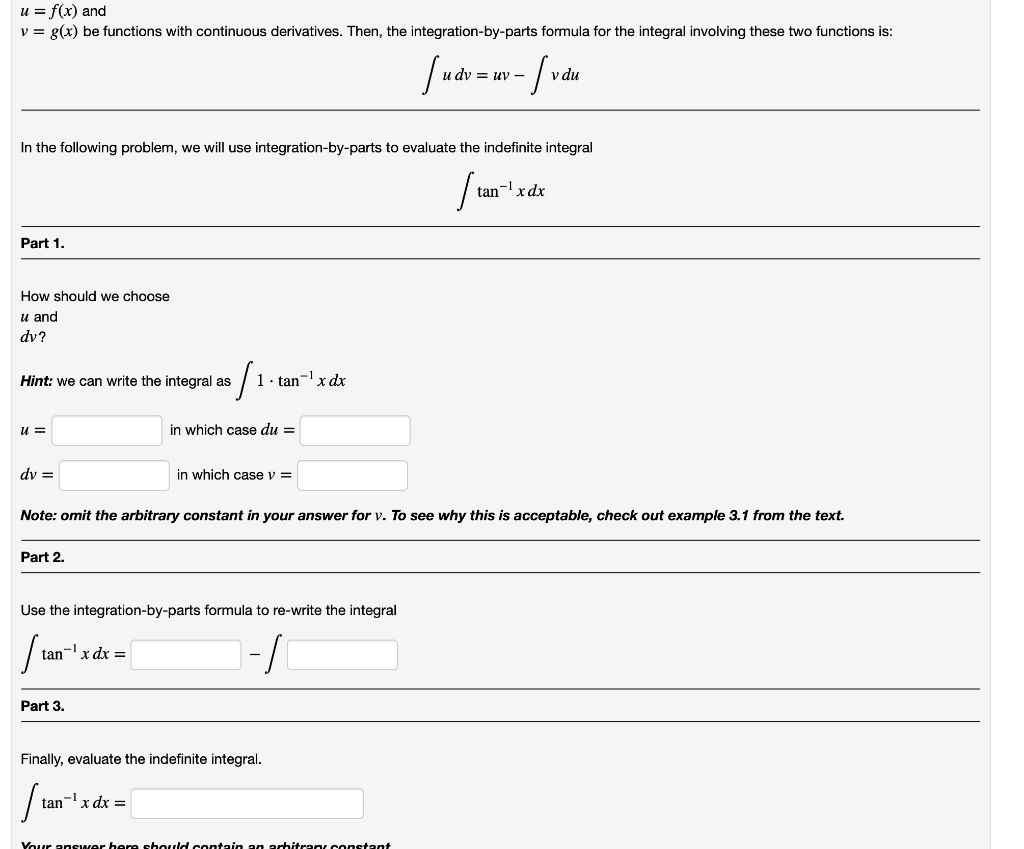



Solved U F X And V G X Be Functions With Continuous D Chegg Com




Unit 4 Integration B C A Study
2R Démonstration Soit Fune primitive de fet soit Gune primitive de g Alors ( F(x) G(x))0= F0(x) G0(x) = f(x) g(x)F(g(x))g′(x)dx by substituting u = g(x) 6 wwwmathcentreacuk 1 c mathcentre 09 1 Introduction There are occasions when it is possible to perform an apparently difficult piece of integration by first making a substitution This has the effect of changing the variable and the integrand When dealing with definite integrals, the limits of integration can also change In this\int \ln(x)\ dx = x\big(\ln(x) 1\big) C\ _\square ∫ ln (x) d x = x (ln (x) − 1) C This shows that an unlikely application of an integration technique can actually be the right way forward!



Calculus Index Cards




Integration By Parts Calculus
X C ∫ 1 1 x 2 d x = arctan x C And since the derivative of a sum is the sum of the derivatives, the integral of a sum is the sum of the integrals ∫ f ( x) g ( x) d x = ∫ f ( x) d x ∫ g ( x) d x And, likewise, constants 'go through' the integral sign ∫ c ⋅ f ( x) d x = c ⋅ ∫ f ( x) d xIntegrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;F x g x dx 0 which implies that a b f x c g x dx 0 for any real c So, we have a b g x 2dx 0 if letting c I b a which implies that g x 0 forall x a,b by (1) That is, f x I b a on a,b (3) Define h x 0ifx 0,1 Q 1 n if x is the rational number m/n (in lowest terms) 1ifx 0 Then h R 0,1 Proof Note that we have shown that h is continuous only at irrational numbers on 0,1 Q We use it to sh




Definite Integral Properties No Graph Function Combination Video Khan Academy




Ppt Integrals Powerpoint Presentation Free Download Id
Here is the formula ∫ f (x)g' (x) dx = f (x)g (x) − ∫ f' (x)g (x) dx You start with the left side of the equation (the antiderivative of the product of two functions) and transform it · Re ∫f (x)g (x)dx Thank you So it is Integration by parts, I guess, just expressed with dv as g (x) And u as f (x) By the way, how come when you take the derivative of something, the dx usually isn't written down, but when you go backwards for the integral, you always write down the dx · From the definition of the definite integral we have, ∫ a a f (x) dx = lim n→∞ n ∑ i=1f (x∗ i)Δx Δx = a−a n = 0 = lim n→∞ n ∑ i=1f (x∗ i)(0) = lim n→∞0 = 0 ∫ a a f ( x) d x = lim n → ∞ ∑ i = 1 n f ( x i ∗) Δ x Δ x = a − a n = 0 = lim n → ∞ ∑ i = 1 n f ( x i ∗) ( 0) = lim n → ∞




Solved 5 6 15 G B Use The Substitution Formula F G X Chegg Com




Finding Derivative With Fundamental Theorem Of Calculus Chain Rule Video Khan Academy
1007 · Given y = f(x) x = f − 1(y) Then ∫f − 1(x)dx = ∫f − 1(y)dy = ∫xdy = ∫xdy dxdx = ∫xf ′ (x)dx = xf(x) − ∫f(x)dx = xf(x) − g(x) C Lastly, we have done integration by parts All the other answers have already given you the finest methods of solving the problemF ′ (x) = f (x) for all x in the interval I There is an infinite number of antiderivatives of a function f (x), all differing only by a constant C (F (x) C)′ = F ′(x) C′ = f (x) 0 = f (x) The set of all antiderivatives for a function f (x) is called the indefinite integral of f (x) and is denoted as ∫ f (x)dx = F (x) C, if F · There is no simple product rule for integration This appropriate and understandable question is almost certainly inspired by the product rule for differentiation, which tells us (f(x) * g(x))' = f'(x) g(x) f(x) g'(x) Unfortunately there is no such simple rule for integration For example, if f(x) = 1/x and g(x) = e^x then we have int \ f(x) \ dx = ln x C int \ g(x) \ dx = e^x




Integration By Parts 𝑒ˣ Cos X Dx Video Khan Academy




Solved Assume That F X And G X Are Continuous And Let F Chegg Com
Integrate x^2 sin y dx dy, x=0 to 1, y=0 to pi;Here is the technique to solve this integration and how to find it#Integral#Integration#Calculus#FormulaTo solve I 1, we will use integration by parts Let the first function = f 1 (x) = f (x) and the second function = g 1 (x) = e x Therefore, I 1 = f (x) ∫ e x dx – ∫ df (x)/dx ∫ e x dx dx Or, I 1 = e x f (x) – ∫ e x f ' (x) dx C Substituting the value of I1 in equation (1), we get




Integration By Parts Proof Udv Uv Vdu Udv Uv Vdu




A Find The Stationary Points Of F X 2x2 3x Chegg Com
Integral Calculus Indefinite Integrals Definition A function F(x) is the antiderivative of a function ƒ(x) if for all x in the domain of ƒ, F'(x) = ƒ(x) ƒ(x) dx = F(x) C, where C is a constantBasic Integration Formulas General and Logarithmic Integrals · Integration Bee Analysis v t e In mathematics, integrals of inverse functions can be computed by means of a formula that expresses the antiderivatives of the inverse f − 1 {\displaystyle f^ {1}} of a continuous and invertible function f {\displaystyle f}Learn how to solve integrals involving logarithmic functions problems step by step online Solve the integral of logarithmic functions int(x^2ln(x))dx We can solve the integral \int x^2\ln\left(x\right)dx by applying integration by parts method to calculate the integral of the product of two functions, using the following formula First, identify u and calculate du




Indefinite Integrals Sums Multiples Video Khan Academy




Practical Integration By Parts Calculus
0121 · Figure 711 To find the area of the shaded region, we have to use integration by parts For this integral, let's choose u = tan − 1x and dv = dx, thereby making du = 1 x2 1 dx and v = x After applying the integrationbyparts formula (Equation 712) we obtain Area = xtan − 1x1 0 − ∫1 0 x x2 1 dxSatz 99 (Partielle Integration) Z f(x)·g0(x)dx = f(x)·g(x) − Z f0(x)·g(x)dx Bemerkung 910 Diese Regel ist in folgender Situation anwendbar • Der Integrand muss das Produkt zweier Funktionen sein • Von einem Faktor (g0(x)) muss man die Stammfunktion g(x) kennen Ein Integral (¨uber f(x) · g0(x)) wird in ein anderes Integral (¨uber f0(x) · g(x)) ¨uberf ¨uhrt, es verbleibtHow to Integrate Compositions of Functions Compositions of functions — that is, one function nested inside another — are of the form f ( g ( x )) You can integrate them by substituting u = g ( x) when You know how to integrate the outer function f The inner function g ( x) differentiates to a constant — that is, it's of the form ax




Copyright C Cengage Learning All Rights Reserved Ppt Download




The Definite Integral And Ftc
Suppose that g(x) is a di erentiable function and f is continuous on the range of g Integration by substitution is given by the following formulas Inde nite Integral Version Z f(g(x))g0(x)dx= Z f(u)du where u= g(x) De nite Integral Version Z b a f(g(x))g0(x)dx= Z g(b) g(a) f(u)du where u= g(x) 11 Example ProblemsBy Literature Title Study Guides Infographics by Subject;




Derivative Of Definite Integrals With Two Limits D Dx X X 2 Cost 2 Dt Chain Rule Ftc1 Youtube




If F A B X F X T H E N Int A B Xf X Dx Is Equal To A B 2
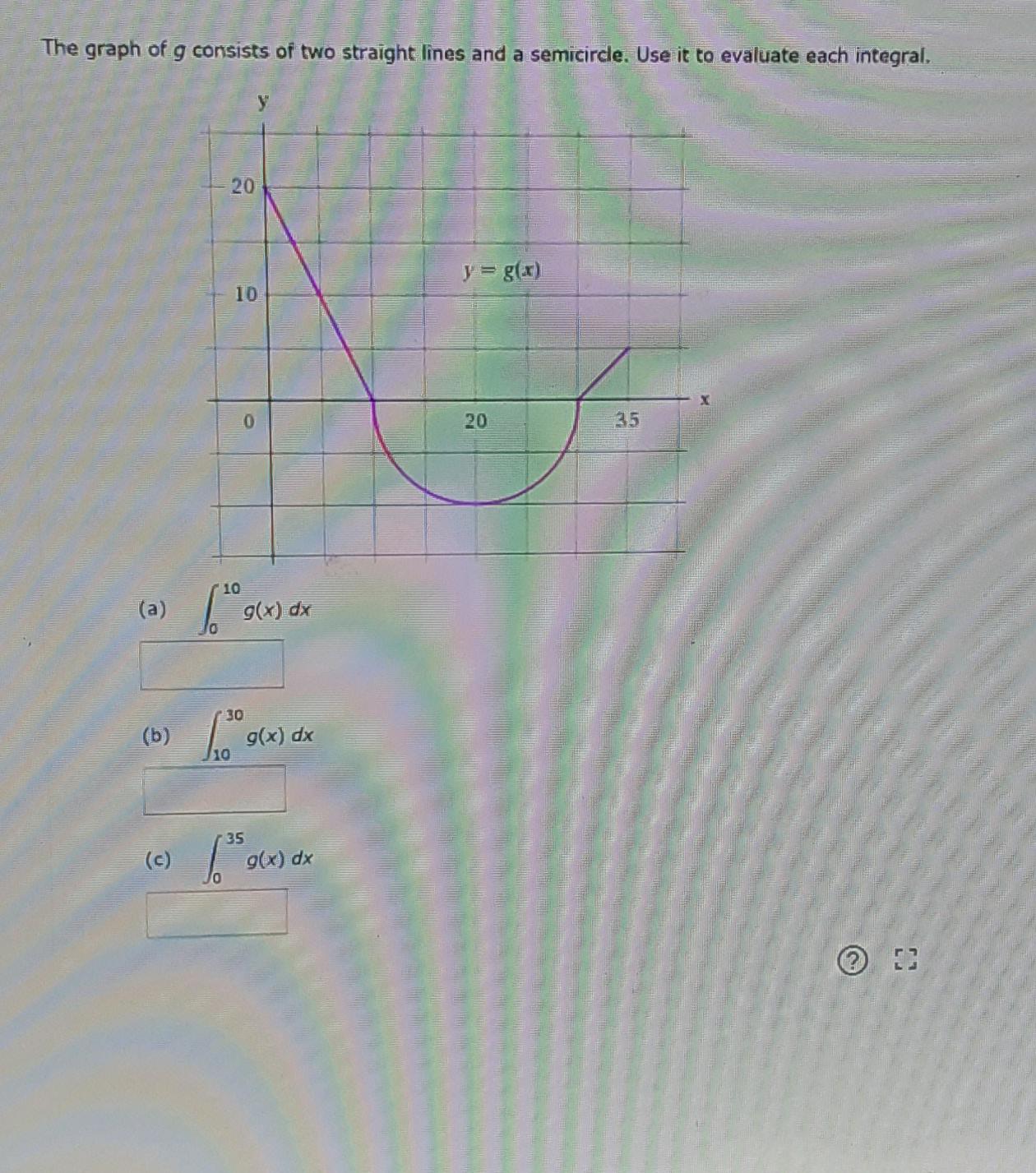



The Graph Of G Consists Of Two Straight Lines And A Semicircle Use It To Eveluate The Integral A Math Int 0 10 G X Dx Math B Math Int 10 30 G X Dx Math C Math Int 0 35 G X Dx Math Homework Help And Answers Slader



Calculus Index Cards




Show That Int 0 A F X G X Dx 2 Int 0 A F X Dx If F And G Define




Integration Of E X Sin X Dx Teachoo Maths Integration Class 12




7 Techniques Of Integration Copyright C Cengage Learning All Rights Reserved Slideshow And Powerpoint Viewer 7 1 Integration By Parts Copyright C Cengage Learning All Rights Reserved




Packet 21 Integration By Parts Ppt Download



Calculus Index Cards



Calculus Index Cards
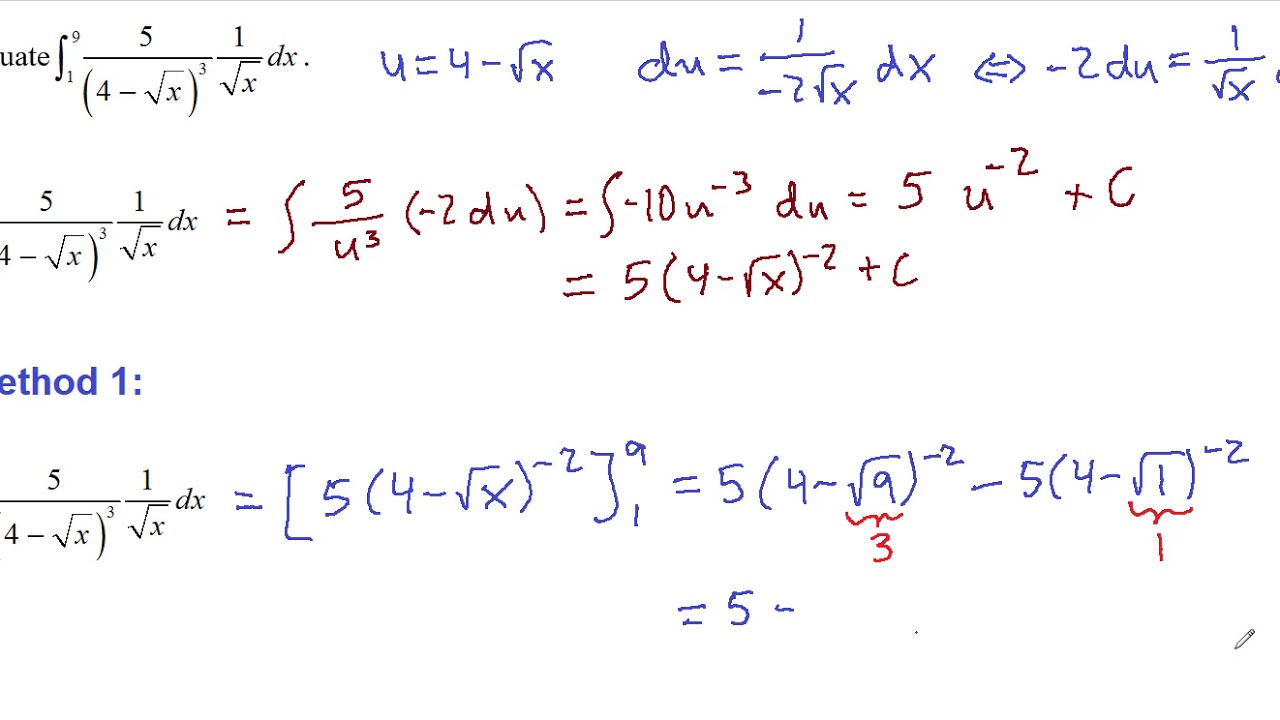



Substitution Rule




Integral Wikipedia




Solved Name Ma 181 Integration By Parts Worksheet Section Chegg Com




Ex 7 9 Direct Integrate X Ex Sin Pi X 4 Dx Ex 7 9
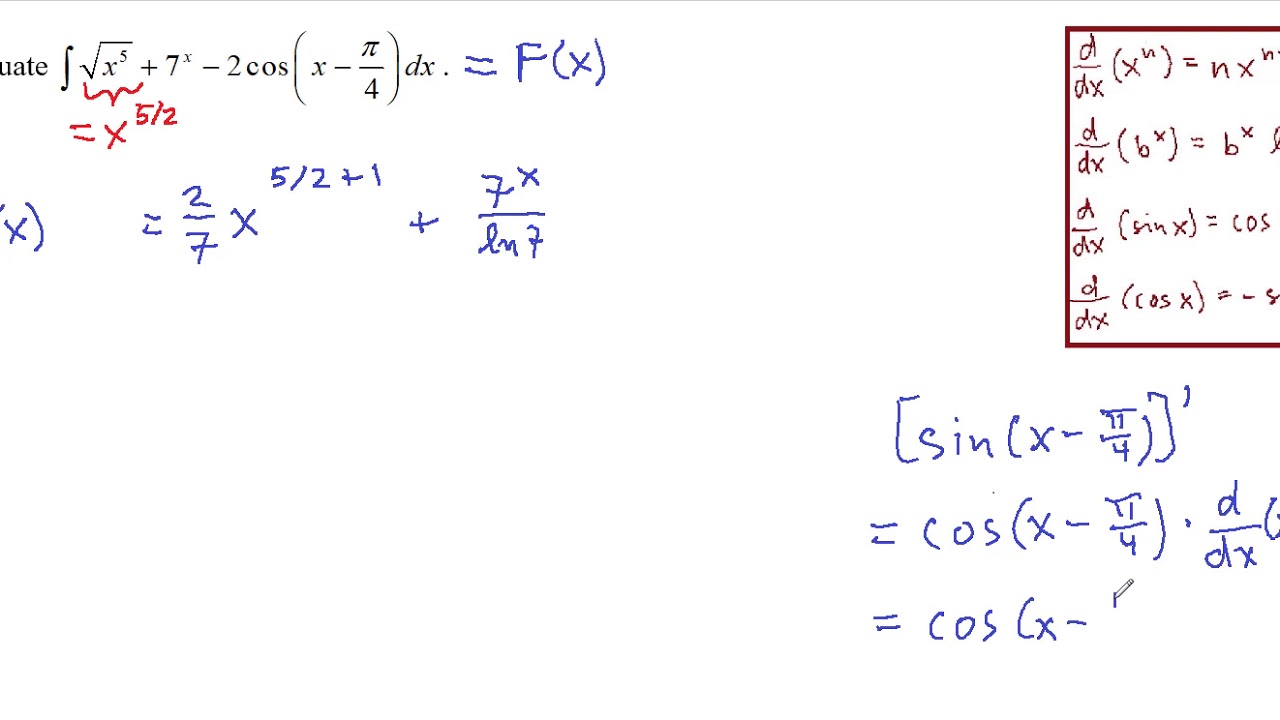



Indefinite Integrals




If D Dx F X G X Then Int F X G X Dx Is Equal To




If Intg X Dx G X Then Intg X F X F X




Packet 21 Integration By Parts Ppt Download




Integration By Parts




Solved 2 A Define F R R And G R R By 21 And G X Chegg Com




Integration By Parts Definite Integrals Video Khan Academy




Find Integration Lnx Or Log X Integration By Parts Teachoo




Ex 7 11 19 Show F X G X Dx 2 F X F X F A X Ex 7 11




Integration By Parts Calculus




Integration By Parts Introduction Youtube




Solved Let F G A B Rightarrow R Be Differentiable Su Chegg Com




If D Dx F X G X Then The Value Of Int A B F X G X Dx Is




Finding Derivative With Fundamental Theorem Of Calculus Video Khan Academy




Misc 35 Prove Definite Integral 0 1 X Ex Dx 1 Miscellaneous




Ex 7 11 19 Show F X G X Dx 2 F X F X F A X Ex 7 11




Integration Review Sheet
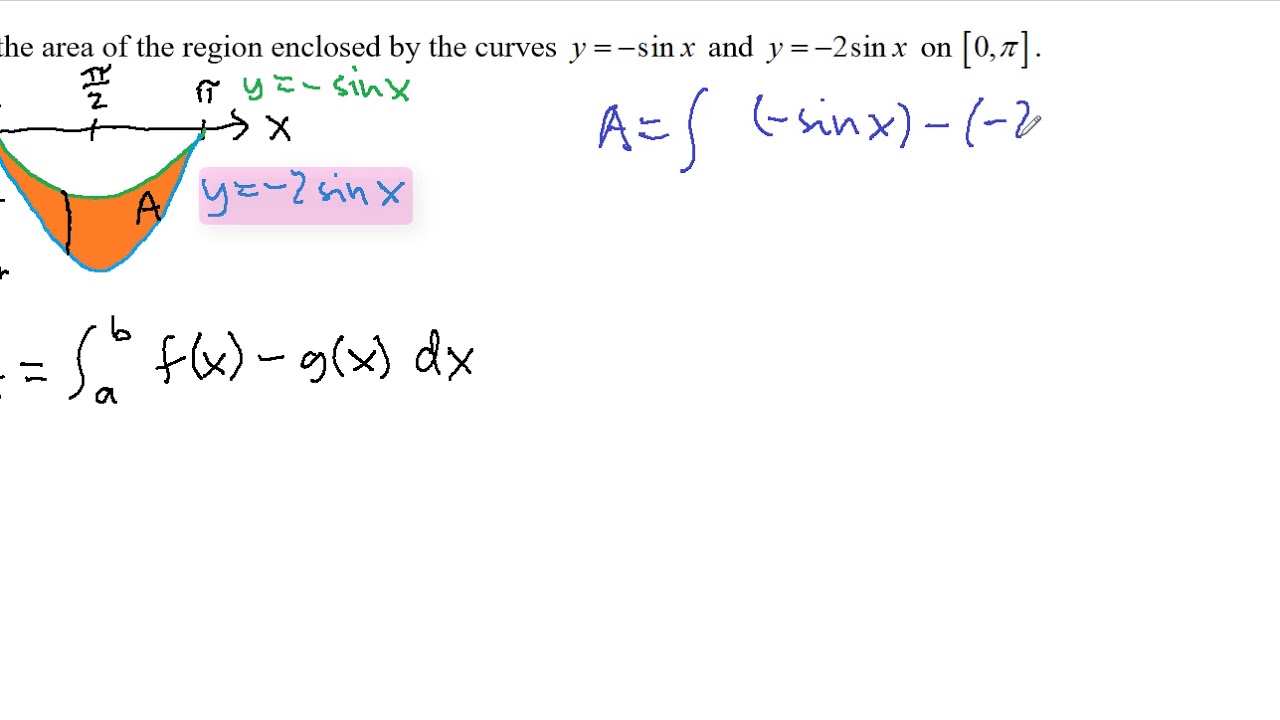



Average Value And Area Revisited




Int E X F X F X Dx Phi X Then Int E X F X Dx Is Youtube




Integration Of E X Sin X Dx Teachoo Maths Integration Class 12




Mat 21b Lecture Integration By Parts Studocu




Integration Theorem F X F X Dx Ln F X C With Proof Youtube




Integral Of The Form Int Xf X F X Dx Can Be Evaluated By Using Integration By Parts In First Youtube



What Is The Integral Of E F X Quora




Integration By Parts Methods Important Notes Videos Solved Examples



0 件のコメント:
コメントを投稿